[Python] 릿지, 라쏘, 엘리스틱넷
in DATA on Data, Python, Python_Data, Ridge, Lasso, Elasticnet
본 페이지는 파이썬 머신러닝 완벽가이드를 공부하며 작성한 내용이다
규제 선형 모델의 개요
- 좋은 머신러닝 회귀 모델이란 데이터에 적합하면서 회귀 계수가 커지는 것을 제한한 모델
- 회귀계수가 커지면 변동성이 심해져 테스트 데이터 세트 예측에서 성능이 저하됨
- 이에 규제 선형 모델은 L1규제, L2규제 등을 활용하여 회귀계수가 커지면 비용함수가 커지도록 식을 구성하여 회귀계수가 커지는 것을 제어함
# 패키지
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from scipy import stats
from sklearn.datasets import load_boston
%matplotlib inline
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score # MSE
# boston 주택 가격 데이터 세트 로드
boston = load_boston()
# boston 데이터 세트 DataFrame으로 변환
df = pd.DataFrame(boston.data, columns=boston.feature_names)
# target값 추가
df["PRICE"] = boston.target
print("boston 데이터 크기 :", df.shape)
df.head(3)
# train test split
y_target = df["PRICE"]
X_data = df.drop("PRICE", axis=1,inplace=False)
X_train, X_test, y_train, y_test = train_test_split(X_data, y_target, test_size=0.3, random_state=156)
boston 데이터 크기 : (506, 14)
릿지 회귀
from sklearn.linear_model import Ridge
from sklearn.model_selection import cross_val_score
# alpha=10
ridge = Ridge(alpha = 10)
neg_mse_scores = cross_val_score(ridge, X_data, y_target, scoring="neg_mean_squared_error", cv=5)
rmse_scores = np.sqrt(-1 * neg_mse_scores)
avg_rmse = np.mean(rmse_scores)
# 결과
print("개별 Negative MSE :", np.round(neg_mse_scores, 2))
print("개별 RMSE :", np.round(rmse_scores,2))
print("rmse 평균 :", np.round(avg_rmse,2))
개별 Negative MSE : [-11.42 -24.29 -28.14 -74.6 -28.52]
개별 RMSE : [3.38 4.93 5.31 8.64 5.34]
rmse 평균 : 5.52
# alpha를 변경하며 수행
alphas = [0,0.1,1,10,100]
for i,alpha in enumerate(alphas):
ridge = Ridge(alpha = alpha)
neg_mse_scores = cross_val_score(ridge, X_data, y_target, scoring="neg_mean_squared_error", cv=5)
rmse_scores = np.sqrt(-1 * neg_mse_scores)
avg_rmse = np.mean(rmse_scores)
print(f"alhpa = {alphas[i]}일 때, rmse 평균 :", np.round(avg_rmse,2))
alhpa = 0일 때, rmse 평균 : 5.83
alhpa = 0.1일 때, rmse 평균 : 5.79
alhpa = 1일 때, rmse 평균 : 5.65
alhpa = 10일 때, rmse 평균 : 5.52
alhpa = 100일 때, rmse 평균 : 5.33
fig, axs = plt.subplots(figsize=(18,6), nrows=1, ncols=5)
coeff_df = pd.DataFrame()
for pos, alpha in enumerate(alphas):
ridge = Ridge(alpha = alpha)
ridge.fit(X_data, y_target)
coeff = pd.Series(ridge.coef_, index=X_data.columns)
col_name = "alpha : "+ str(alpha)
coeff_df[col_name] = coeff
# 막대그래프
coeff = coeff.sort_values(ascending=False)
axs[pos].set_title(col_name)
axs[pos].set_xlim(-10,10)
sns.barplot(x=coeff.values, y=coeff.index, ax=axs[pos])
plt.show()
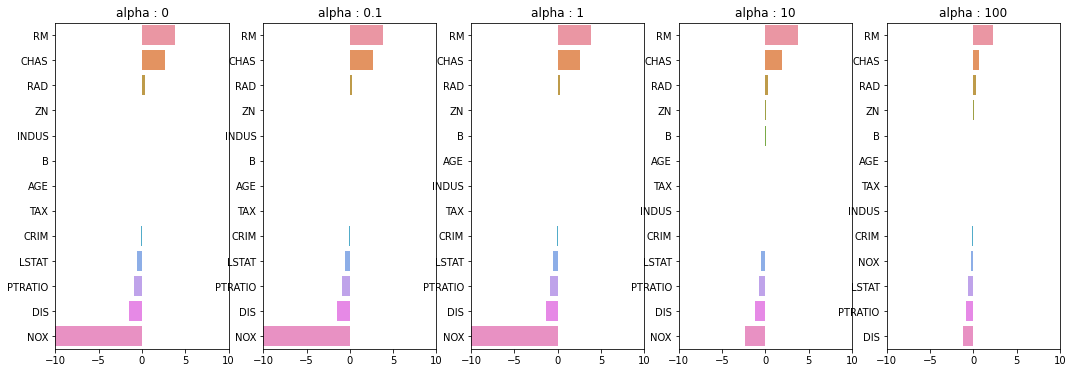
- alpha를 높일수록 NOX의 회귀계수 값이 줄어듬
라쏘 회귀
from sklearn.linear_model import Lasso, ElasticNet
def get_linear_reg_eval(model_name, params=None, X_data_n=None, y_target_n=None, verbose=True, return_coeff=True):
coeff_df = pd.DataFrame()
if verbose : print("#####", model_name, "#####")
for param in params:
if model_name == "Ridge" : model = Ridge(alpha=param)
elif model_name == "Lasso" : model = Lasso(alpha=param)
elif model_name == "ElasticNet" : model = ElasticNet(alpha=param, l1_ratio=0.7)
neg_mse_scores = cross_val_score(model, X_data_n,y_target_n, scoring = "neg_mean_squared_error", cv = 5)
avg_rmse = np.mean(np.sqrt(-1 * neg_mse_scores))
print(f"alpha {param}일 때 평균 RMSE = {avg_rmse:.3f}")
# cross_val_score는 evaluation metric만 반환하므로 모델을 재학습하여 회귀계수 추출
model.fit(X_data_n, y_target_n)
if return_coeff:
coeff = pd.Series(data=model.coef_, index=X_data.columns)
colname="alpha : "+str(param)
coeff_df[colname] = coeff
return coeff_df
lasso_alphas = [0.01,0.07,0.1,0.5,1,3,5,10]
coeff_lasso_df = get_linear_reg_eval("Lasso", params=lasso_alphas, X_data_n=X_data, y_target_n=y_target)
##### Lasso #####
alpha 0.01일 때 평균 RMSE = 5.740
alpha 0.07일 때 평균 RMSE = 5.612
alpha 0.1일 때 평균 RMSE = 5.615
alpha 0.5일 때 평균 RMSE = 5.669
alpha 1일 때 평균 RMSE = 5.776
alpha 3일 때 평균 RMSE = 6.189
alpha 5일 때 평균 RMSE = 6.375
alpha 10일 때 평균 RMSE = 6.586
sort_column = "alpha : "+str(lasso_alphas[0])
coeff_lasso_df.sort_values(by=sort_column, ascending=False)
| alpha : 0.01 | alpha : 0.07 | alpha : 0.1 | alpha : 0.5 | alpha : 1 | alpha : 3 | alpha : 5 | alpha : 10 | |
|---|---|---|---|---|---|---|---|---|
| RM | 3.814186 | 3.789725 | 3.703202 | 2.498212 | 0.949811 | 0.000000 | 0.000000 | 0.000000 |
| CHAS | 2.504190 | 1.434343 | 0.955190 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| RAD | 0.298526 | 0.270936 | 0.274707 | 0.277451 | 0.264206 | 0.061864 | 0.000000 | 0.000000 |
| ZN | 0.046860 | 0.049059 | 0.049211 | 0.049544 | 0.049165 | 0.037231 | 0.038467 | 0.026146 |
| B | 0.009485 | 0.010248 | 0.010249 | 0.009469 | 0.008247 | 0.006510 | 0.006286 | 0.007496 |
| INDUS | 0.006474 | -0.042120 | -0.036619 | -0.005253 | -0.000000 | -0.000000 | -0.000000 | -0.000000 |
| AGE | -0.001818 | -0.011706 | -0.010037 | 0.003604 | 0.020910 | 0.042495 | 0.031679 | 0.000000 |
| TAX | -0.012627 | -0.014290 | -0.014570 | -0.015442 | -0.015212 | -0.008602 | -0.007669 | -0.009282 |
| CRIM | -0.106228 | -0.098193 | -0.097894 | -0.083289 | -0.063437 | -0.000000 | -0.000000 | -0.000000 |
| LSTAT | -0.530481 | -0.560431 | -0.568769 | -0.656290 | -0.761115 | -0.807679 | -0.747258 | -0.564038 |
| PTRATIO | -0.916369 | -0.765107 | -0.770654 | -0.758752 | -0.722966 | -0.265072 | -0.000000 | -0.000000 |
| DIS | -1.422155 | -1.176583 | -1.160538 | -0.936605 | -0.668790 | -0.000000 | -0.000000 | -0.000000 |
| NOX | -14.394478 | -0.000000 | -0.000000 | -0.000000 | -0.000000 | 0.000000 | 0.000000 | 0.000000 |
ElasticNet
elastic_alphas = [0.07, 0.1, 0.5, 1, 3]
coeff_elastic_df = get_linear_reg_eval("ElasticNet", params=elastic_alphas, X_data_n=X_data, y_target_n=y_target)
##### ElasticNet #####
alpha 0.07일 때 평균 RMSE = 5.542
alpha 0.1일 때 평균 RMSE = 5.526
alpha 0.5일 때 평균 RMSE = 5.467
alpha 1일 때 평균 RMSE = 5.597
alpha 3일 때 평균 RMSE = 6.068
# method는 Standar, Minax, Log 결정
from sklearn.preprocessing import StandardScaler, MinMaxScaler # Scaler
from sklearn.preprocessing import PolynomialFeatures
def get_scaled_data(method="None", p_degree=None, input_data=None):
if method == "Standard":
scaled_data = StandardScaler().fit_transform(input_data)
elif method == "MinMax":
scaled_data = MinMaxScaler().fit_transform(input_data)
elif method == "Log":
scaled_data = np.log1p(input_data)
else:
scaled_data = input_data
if p_degree != None:
scaled_data = PolynomialFeatures(degree=p_degree, include_bias=False).fit_transform(scaled_data)
return scaled_data
alphas = [0.1, 1, 10, 100]
scale_methods = [(None, None), ("Standard",None), ("Standard",2), ("MinMax", None), ("MinMax", 2), ("Log", None)]
for scale_method in scale_methods:
X_data_scaled = get_scaled_data(method=scale_method[0], p_degree=scale_method[1], input_data=X_data)
print("\n ## 변환 유형 : {0}, Polynomial Degree:{1}".format(scale_method[0], scale_method[1]))
get_linear_reg_eval("Ridge", params=alphas, X_data_n=X_data_scaled, y_target_n=y_target, verbose=False, return_coeff=False)
## 변환 유형 : None, Polynomial Degree:None
alpha 0.1일 때 평균 RMSE = 5.788
alpha 1일 때 평균 RMSE = 5.653
alpha 10일 때 평균 RMSE = 5.518
alpha 100일 때 평균 RMSE = 5.330
## 변환 유형 : Standard, Polynomial Degree:None
alpha 0.1일 때 평균 RMSE = 5.826
alpha 1일 때 평균 RMSE = 5.803
alpha 10일 때 평균 RMSE = 5.637
alpha 100일 때 평균 RMSE = 5.421
## 변환 유형 : Standard, Polynomial Degree:2
alpha 0.1일 때 평균 RMSE = 8.827
alpha 1일 때 평균 RMSE = 6.871
alpha 10일 때 평균 RMSE = 5.485
alpha 100일 때 평균 RMSE = 4.634
## 변환 유형 : MinMax, Polynomial Degree:None
alpha 0.1일 때 평균 RMSE = 5.764
alpha 1일 때 평균 RMSE = 5.465
alpha 10일 때 평균 RMSE = 5.754
alpha 100일 때 평균 RMSE = 7.635
## 변환 유형 : MinMax, Polynomial Degree:2
alpha 0.1일 때 평균 RMSE = 5.298
alpha 1일 때 평균 RMSE = 4.323
alpha 10일 때 평균 RMSE = 5.185
alpha 100일 때 평균 RMSE = 6.538
## 변환 유형 : Log, Polynomial Degree:None
alpha 0.1일 때 평균 RMSE = 4.770
alpha 1일 때 평균 RMSE = 4.676
alpha 10일 때 평균 RMSE = 4.836
alpha 100일 때 평균 RMSE = 6.241
