Tidymodels로 시작하는 머신러닝 (1)
in DATA on Data, Machine Learning, Tidymodels, Parsnip, 타이디모델, R-machine-learning
개요
Tidymodel의 모델 빌딩에 대해서 살펴봅니다.
- 관련 포스트
- 목차
TidyModel을 접하고 생각한 것은 ‘정말 많이 편하게 만드려고 노력했구나’였습니다. 예를 들어서 이전에는 로지스틱회귀분석과 RandomForest의 모델링을 위해서는 전혀 다른 패키지와 전혀다른 프로세스를 태워야 했습니다. 하지만 지금 Tidymodel에서는 몇 가지 공통된 패키지에서 여러 모델들을 해결할 수 있습니다.
데이터분석을 공부함에 있어서 R을 선택해야 할 지 파이썬을 선택해야 할 지 고민의 기로에 섰던 때가 있었습니다. 사실 지금 시점에서 데이터분석을 하자면, 다른 사람이 만든 코드의 해석을 위해서라도 파이썬을 공부해야 하는 위치에 있긴 하지만, 어쨌든 R만으로도 부족함 없이 데이터 분석을 할 수 있을 것이라는 생각이 확연히 들었습니다.
본 서는 https://www.tidymodels.org/start/models/의 내용을 요약했습니다. 영어로 되어 있는 내용을 옮기는 수준이지만, 그 안에서 제가 느낀 궁금증을 좀더 정리해볼 예정입니다.
- 모든 공부에 기본베이스는 필요하지만, 어느 정도 배우고 나서는 꼭 수학공식 배우듯이 밑에서부터 쌓아야 할 이유는 없다고 생각합니다. 직접 업무를 수행하듯이 하면서 필요한 것들을 끼워넣으며 배우는 게 더욱 실무에는 효율적인 방법이라고 생각합니다. 그래서 앞으로는 머신러닝을 Tidymodel로 풀어가면서 중간중간 마주치는 통계개념과 방법론을 조금씩 정리해나갈 생각입니다.
라이브러리 로드
library(tidymodels)
tidymodel우리의 메인패키지,parsnip이라는 패키지를 통해 모델링을 돕습니다.readr패키지는 테이블 형태의 데이터를 좀더 친숙하고 편하게 불러들이기 위해 사용합니다.- https://cran.r-project.org/web/packages/readr/readme/README.html
데이터 로드
urchins <- read_csv("https://tidymodels.org/start/models/urchins.csv") %>%
setNames(c("food_regime", "initial_volume", "width")) %>%
mutate(food_regime = factor(food_regime, levels = c("Initial", "Low", "High")))
##
## -- Column specification ---------------------------------------------------------------------------------------
## cols(
## TREAT = col_character(),
## IV = col_double(),
## SUTW = col_double()
## )
- 데이터 소개
- urchins데이터는 성게와 관련된 데이터
- initial_volume : 성게의 초기 사이즈
- food_regime : 먹이를 주는 그룹의 분류
- width : 성체의 사이즈, 여기서는 종속변수가 된다.
setNames함수를%>%를 통해 적용하여 데이터의 이름을 바꿔줍니다. 원래는 TREAT,IV,SUTW를 Column Name으로 하는 데이터이며, 벡터화시켜서 차례대로 적용된 것을 확인할 수 있습니다.mutate를 통해서 character를 factor로 데이터 타입 변경- urchins 데이터는
tibble형태임. tibble은 Data.Frame보다 더 정리된 형태이며 tidyverse의 패키지와 상호호환되기 좋은 데이터 형태
시각화
urchins %>%
ggplot(aes(x = initial_volume, y = width, col = food_regime))+
geom_point() +
geom_smooth(method = lm, se = F)
## `geom_smooth()` using formula 'y ~ x'
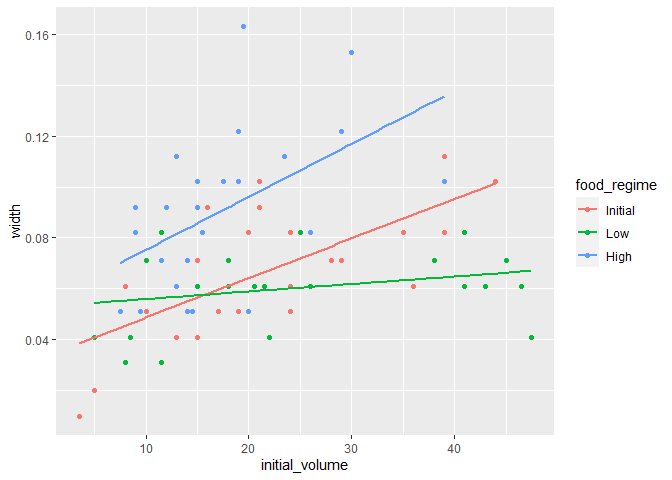
- 시각화 결과 initial_volume에 따른 width크기의 변화가 분명히 존재하며, food_regime에 따라서 기울기가 다르게 나타남을 알 수 있습니다.
모델 만들기
width ~ initial_volume *food_regime
위와 같은 형태로 데이터를 짜면 food_regime에 따라서 각각의 기울기(slope)와 절편(intercept)을 구할 수 있습니다. 이제 여기서 parsnip 패키지를 사용해봅시다. 우리는 Regression 즉 예측값을 추정해보고 싶으므로 회귀분석(Linear Regression)을 시행합니다.
lr_mod <-
linear_reg() %>% # 모델 특정하기
set_engine('lm')
- 먼저 모델을 선언해줍니다. 여기서는
linear_reg()이라고 선형귀모델을 선언했습니다. - set engine은 어떤 패키지나 컴퓨팅시스템을 통해서 모델을 훈련시킬 것인지 지정하는 것입니다.
lm_fit <-
lr_mod %>%
fit(width ~ initial_volume*food_regime, data = urchins)
tidy(lm_fit)
## # A tibble: 6 x 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 0.0331 0.00962 3.44 0.00100
## 2 initial_volume 0.00155 0.000398 3.91 0.000222
## 3 food_regimeLow 0.0198 0.0130 1.52 0.133
## 4 food_regimeHigh 0.0214 0.0145 1.47 0.145
## 5 initial_volume:food_regimeLow -0.00126 0.000510 -2.47 0.0162
## 6 initial_volume:food_regimeHigh 0.000525 0.000702 0.748 0.457
fit()을 통해서 모델을 쉽게 fitting 가능합니다.tidy함수를 통해서 피팅한 결과를 깔끔한 테이블 형태로 볼 수 있습니다.
tidy(lm_fit) %>%
dwplot(dot_args = list(size = 2, color = "black"),
whisker_args = list(color = "black"),
vline = geom_vline(xintercept = 0, colour = "grey50", linetype = 2))
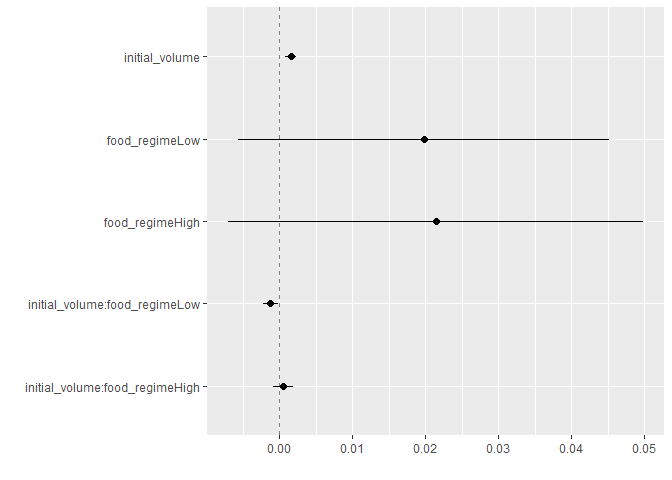
dwplot은 dot-whisker-plot의 약자입니다. 이 plot은 fitting한 모델의 coefficient estimate의 결과를 점으로, 95% 신뢰구간을 whisker(수염)으로 표현해줍니다.- 하지만 이 그래프만을 보고 P-Value, 즉 유효성을 볼 수는 없는 것처럼 보입니다.
- 참고자료
Prediction
urnchins데이터는 lm_fit 객체 안에 학습되어 있습니다. 이를 바탕으로 새로운 데이터가 있다고 가정하고 모델링을 진행하겠습니다.
new_points <- expand.grid(initial_volume =20,
food_regime = c('Initial','Low','High'))
new_points
## initial_volume food_regime
## 1 20 Initial
## 2 20 Low
## 3 20 High
expand.grid함수는 data.frame을 만들어주는 함수입니다. 그냥data.frame과 다른점은 factor를 기준으로 데이터를 여러 번 반복해서 출력해준다는 점입니다. 아래 예시를 통해서 보면 차이점이 확연해집니다.
data.frame(x=1:5, y=letters[1:5])
## x y
## 1 1 a
## 2 2 b
## 3 3 c
## 4 4 d
## 5 5 e
expand.grid(x=1:5, y=letters[1:5])
## x y
## 1 1 a
## 2 2 a
## 3 3 a
## 4 4 a
## 5 5 a
## 6 1 b
## 7 2 b
## 8 3 b
## 9 4 b
## 10 5 b
## 11 1 c
## 12 2 c
## 13 3 c
## 14 4 c
## 15 5 c
## 16 1 d
## 17 2 d
## 18 3 d
## 19 4 d
## 20 5 d
## 21 1 e
## 22 2 e
## 23 3 e
## 24 4 e
## 25 5 e
Tidymodel에서는 predicted_value, 즉 예측값의 포멧이 똑같습니다.
mean_pred <- predict(lm_fit, new_data = new_points)
mean_pred
## # A tibble: 3 x 1
## .pred
## <dbl>
## 1 0.0642
## 2 0.0588
## 3 0.0961
- tibble은 언제나 정리된 데이터 형식을 출력합니다. 따라서
predict의 값들도 정해진 포멧이 있습니다. 이렇게 포멧이 통일되어 있으면, 언제든 다른 방법으로 만들어낸 데이터와 Combine하여 결과를 보기 좋은 점이 있습니다.
conf_int_pred <- predict(lm_fit,
new_data = new_points,
type = 'conf_int')
conf_int_pred
## # A tibble: 3 x 2
## .pred_lower .pred_upper
## <dbl> <dbl>
## 1 0.0555 0.0729
## 2 0.0499 0.0678
## 3 0.0870 0.105
# Combine Data
bind_cols(new_points,mean_pred, conf_int_pred)
## initial_volume food_regime .pred .pred_lower .pred_upper
## 1 20 Initial 0.06421443 0.05549934 0.07292952
## 2 20 Low 0.05880940 0.04986251 0.06775629
## 3 20 High 0.09613343 0.08696233 0.10530453
- conf_int_pred라는 객체에 신뢰구간을 부여했습니다.
- 여기서
bind_cols함수를 통해서 column들을 기준으로 데이터를 합쳐줄 수 있었습니다. 하지만 여기 서 잠깐, 이걸 pipe operater(%>%)를 통해서 표현하면 어떻게 될까요? 놀람게도 같은 결과를 볼 수 있습니다. 보시는 바와 같이, pipe operator의 강점은 사람의 인지능력과 유사하게 함수를 쌓아나갈 수 있다는 점입니다. - 앞서 설명했듯,
tibble형태의 데이터에서는 신뢰구간이.pred_lower,.pred_upper처럼 정형화된 컬럼명이 정의됩니다.
plot_data <-
new_points %>%
bind_cols(mean_pred) %>%
bind_cols(conf_int_pred)
plot_data
## initial_volume food_regime .pred .pred_lower .pred_upper
## 1 20 Initial 0.06421443 0.05549934 0.07292952
## 2 20 Low 0.05880940 0.04986251 0.06775629
## 3 20 High 0.09613343 0.08696233 0.10530453
# 그래프
ggplot(plot_data, aes(x = food_regime)) +
geom_point(aes(y = .pred)) +
geom_errorbar(aes(ymin = .pred_lower,
ymax = .pred_upper),
width = .2) +
labs(y = "성게 사이즈")
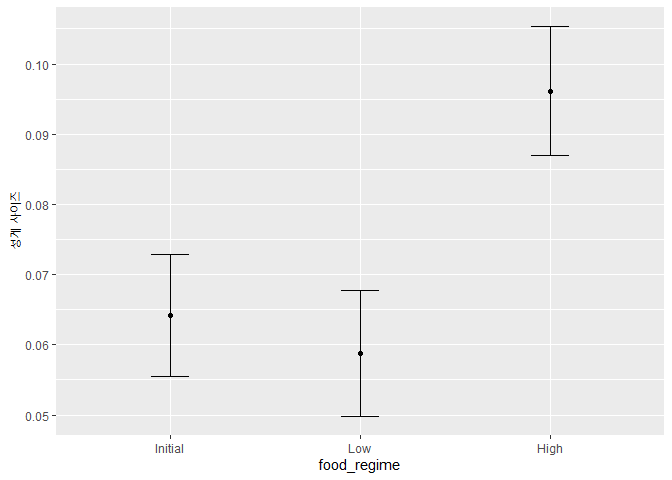
다른 모델링 적용해보기
지금까지는 회귀분석으로 모두가 만족할만한 결과를 냈습니다. 하지만 베이지안 통계 신봉자는 베이지안 모델링을 사용하고 싶을 수 있겠죠. 보통 이렇게 모델링을 바꿀 경우, 일반적으로 전혀 다른 프로세스와 패키지를 사용해야 합니다. 하지만 tidymodel에서는 유사한 모델피팅 과정을 통해 베이지안 회귀분석을 수행할 수 있습니다.
베이지안 통계에서는 사전분포가 필요합니다. 만약 분석가들이 이 분포가코시 분포 (자유도가 1인 t 분포) 인 것에 합의했다고 가정해보겠습니다.
# t사전 분포 정의
prior_dist <- rstanarm::student_t(df = 1)
set.seed(123)
# parsnip 모델 정의
bayes_mod <-
linear_reg() %>%
set_engine("stan",
prior_intercept = prior_dist,
prior = prior_dist)
# 모델 훈련
bayes_fit <-
bayes_mod %>%
fit(width ~ initial_volume * food_regime, data = urchins)
# 결과 보기기
tidy(bayes_fit)
## # A tibble: 6 x 3
## term estimate std.error
## <chr> <dbl> <dbl>
## 1 (Intercept) 0.0334 0.00926
## 2 initial_volume 0.00155 0.000400
## 3 food_regimeLow 0.0195 0.0127
## 4 food_regimeHigh 0.0206 0.0150
## 5 initial_volume:food_regimeLow -0.00125 0.000506
## 6 initial_volume:food_regimeHigh 0.000560 0.000704
- 먼저 사전분포를 정의했다. 사전분포는
rstanarm패캐지에서 t-분포로 지정합니다. linear_reg()를 통해 회귀 모델링임을 선언하고set_engine을 통해서stan패키지의 엔진을 도입합니다. 이 때 베이지안 통계임을 염두해두고,prior_intercept(사전분포 절편)와prior(사전분포)을 함께 정의합니다.- 똑같이 formula를 적용해 모델을 적합한 후,
tidy()함수를 통해 결과를 살펴봅니다. 그냥 결과를 print해서 보는 것 보다 훨씬 정리된 형태로 보여주는 것을 알 수 있습니다.tidymodels()패키지의 목적 자체가 프로세스와 결과의 일관화입니다.
bayes_plot_data <-
new_points %>%
bind_cols(predict(bayes_fit, new_data = new_points)) %>%
bind_cols(predict(bayes_fit, new_data = new_points, type = "conf_int"))
ggplot(bayes_plot_data, aes(x = food_regime)) +
geom_point(aes(y = .pred)) +
geom_errorbar(aes(ymin = .pred_lower, ymax = .pred_upper), width = .2) +
labs(y = "성게 사이즈") +
ggtitle("자유도 1의 t-분포 하의 베이지안 회귀분석")
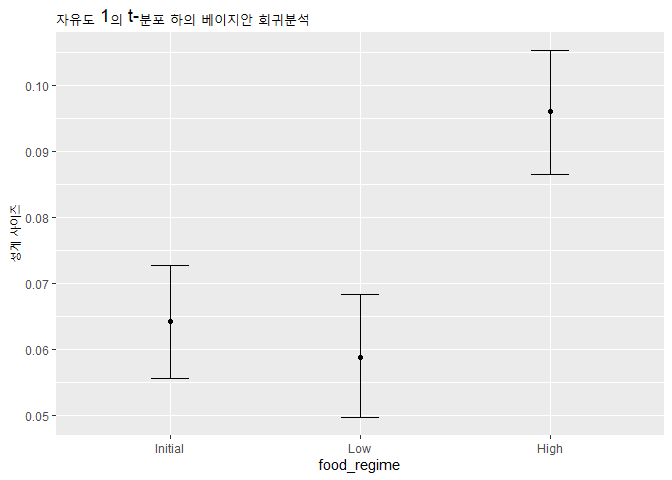
- 위 과정은 앞서 진행한 회귀분석의 plot_data 작성 과정과 동일하므로 생략
결론
이 패키지를 통해서 우리는 아래와 같은 것을 배울 수 있었습니다.
tidymodels를 통해서 머신러닝 프로세스를 R 상에서 일원화 할 수 있습니다.- 다른 패키지의 도입 없이 하나의 패키지 플랫폼에서 머신러닝 과정을 처리 가능합니다.
- 이전보다 조금 더 깔끔해졌습니다… :)
이어지는 정리에서는 recipe를 살펴볼 예정입니다. 이 과정을 통해서 전처리 과정이 얼마나 간단하게 진행되어서 모델링 자체에 집중할 수 있게 되는지 한 번 파악해보겠습니다.
